Which Set Of Angles Can Form A Triangle | What Type Of Angle Can Form A Triangle?

Let’s explore the fascinating world of triangles and the angles that make them unique!

Right Angle Triangles have one right angle (90 degrees). The other two angles always add up to 90 degrees to make a total of 180 degrees in the triangle.

Isosceles Triangles have two equal sides and two equal angles.

Equilateral Triangles are special because all three sides are equal, and all three angles are 60 degrees each.

Scalene Triangles are the most versatile. They have three different side lengths and three different angles.

The Triangle Inequality Theorem is a fundamental rule in geometry. It states that the sum of any two sides of a triangle must be greater than the length of the third side. This rule helps us understand why certain angles can form triangles, while others cannot.

To understand why specific types of angles create different triangles, let’s visualize the angles within a triangle. The angles inside any triangle always add up to 180 degrees.

Right Angle Triangle: The presence of a right angle (90 degrees) means the other two angles must be acute angles (less than 90 degrees) to maintain the 180-degree sum.
Isosceles Triangle: If two angles are equal, and the total must be 180 degrees, you can calculate the angles.
Equilateral Triangle: All angles are equal, and the sum is 180 degrees, so each angle must be 60 degrees.
Scalene Triangle: Since all angles are different, you can have various combinations of angles, as long as they add up to 180 degrees.

So, when we talk about the types of angles that can form a triangle, it all boils down to the sum of the angles, which must always be 180 degrees! Remember the Triangle Inequality Theorem and the specific angle properties of each triangle type. This will help you identify and understand the unique characteristics of different triangles.

We know that the sum of all three interior angles in a triangle is always 180 degrees. An acute angle is an angle that measures less than 90 degrees. So, a triangle can have three acute angles, meaning all three angles measure less than 90 degrees.

Let’s dive a little deeper into this. A triangle with three acute angles is called an acute triangle. This is just one type of triangle based on the types of angles it has. You can also have triangles with one right angle (a right triangle) or one obtuse angle (an obtuse triangle). An obtuse angle measures more than 90 degrees.

There are many different combinations of angles that can form a triangle, but they all must add up to 180 degrees. Here are some examples:

Acute triangle: 60 degrees, 60 degrees, 60 degrees (an equilateral triangle)
Acute triangle: 45 degrees, 45 degrees, 90 degrees (an isosceles right triangle)
Right triangle: 30 degrees, 60 degrees, 90 degrees
Obtuse triangle: 30 degrees, 40 degrees, 110 degrees

As you can see, there are many different combinations of angles that can form a triangle, but they all have to follow the rule that the sum of the angles must equal 180 degrees.

Let’s talk about triangles! You’re curious about whether two acute angles and one obtuse angle can form a triangle.

It’s not possible to have more than one obtuse angle in a triangle. The angles inside any triangle always add up to 180 degrees. If you already have one obtuse angle (greater than 90 degrees), the other two angles have to be smaller than 90 degrees to keep the total at 180 degrees. That means they have to be acute!

Here’s a way to picture it:

* Imagine a triangle where one angle is 120 degrees (obtuse). The other two angles must add up to 60 degrees (180 – 120 = 60).
* Since both of the remaining angles must be less than 90 degrees, they have to be acute!

So, to summarize, a triangle can only have one obtuse angle, and the other two angles will always be acute. This is a fundamental property of triangles in Euclidean geometry.

The angles 80°, 40°, 60° can form a triangle.

Let’s dive a bit deeper into why this is the case. To form a triangle, the sum of the interior angles must always equal 180°. Let’s check:

80° + 40° + 60° = 180°

Since the sum of these angles is 180°, we know they can form a triangle. This is a key principle in geometry, and it’s important to remember when working with triangles.

We all know that triangles are three-sided shapes, but did you know that the angles inside a triangle always add up to 180 degrees? This is a fundamental rule in geometry, and it’s super helpful for understanding and solving problems related to triangles.

Let’s break down why this is true: Imagine a triangle with three corners (or vertices). Each corner has an interior angle which is the angle inside the triangle at that corner. At each corner, there is also an exterior angle, which is the angle formed by extending one side of the triangle. The interior and exterior angles at each corner form a straight line, so they add up to 180 degrees. If you add up all three interior angles and all three exterior angles, you get a total of 540 degrees. Since each interior and exterior angle pair adds up to 180 degrees, the three interior angles must add up to 180 degrees!

Now, let’s talk about isosceles triangles. These special triangles have two sides that are the same length, and those two sides create two equal angles. This means that the two angles opposite the equal sides are also equal. This is a really handy piece of information when you’re working with isosceles triangles.

For example, if you know that one angle in an isosceles triangle is 60 degrees, and you know that the other two angles are equal, then you can use the rule that all angles in a triangle add up to 180 degrees to figure out that each of the other two angles is 60 degrees. This means that the triangle is a special type of isosceles triangle called an equilateral triangle, where all three sides and all three angles are equal!

You can’t form a unique triangle using only three angles. Why? Because triangles have flexible sides that can change length. Think about it like this: If you have three angles, you can have a small triangle, a large triangle, or even a giant triangle. All those triangles could have the same three angles but be different sizes.

To make a unique triangle, you need some information about the sides too! You can create a unique triangle with:

All three sides (Side-Side-Side)
Two sides and the included angle (Side-Angle-Side)

What’s the “included angle”? It’s the angle that’s formed by the two sides you’re given.

Let’s look at this with an example. Imagine you have a triangle with a 60° angle, a 70° angle, and a 50° angle. Now, picture a second triangle with the same angles but smaller sides. Both triangles have the same angles but are different sizes, meaning they’re not the same triangle.

Key takeaway: To have a unique triangle, you need information about both angles and sides.

You can create a triangle using three line segments. But not just any three segments will work! You need to be sure that the sum of the lengths of any two sides is greater than the length of the remaining side.

Let’s look at an example. Say you have three line segments with lengths of 3, 4, and 5.

3 + 4 > 5 (True)
3 + 5 > 4 (True)
4 + 5 > 3 (True)

Since the sum of the lengths of any two sides is greater than the length of the third side, these three line segments will form a triangle!

But let’s try another set of segments with lengths 2, 3, and 6.

2 + 3 > 6 (False)

Since the sum of the lengths of the two shorter segments is not greater than the length of the longest segment, these three segments will not form a triangle.

This is known as the Triangle Inequality Theorem. It’s a fundamental rule in geometry that tells us which sets of line segments can be used to construct a triangle.

Think of it like trying to build a triangle out of sticks. If you try to make a triangle with sticks that are too short, or one that is too long, you won’t be able to connect them to form a closed shape. The sticks need to be just the right lengths to form a triangle.

Remember, the Triangle Inequality Theorem applies to all triangles, regardless of whether they are right triangles, obtuse triangles, or acute triangles. So, you can use it to determine if any set of three line segments can form a triangle!

We all know that triangles have three angles. And a super cool fact is that all three angles in any triangle always add up to 180 degrees. Isn’t that neat?

Let’s say you know two of the angles in a triangle. To find the missing angle, just add the two angles you know together. Then, subtract that sum from 180 degrees, and voila! You’ve got the missing angle.

For example, let’s say a triangle has an angle A of 60 degrees and an angle B of 84 degrees. To find angle C, we’d do the following:

1. Add angle A and angle B: 60 degrees + 84 degrees = 144 degrees
2. Subtract the sum from 180 degrees: 180 degrees – 144 degrees = 36 degrees

So, angle C is 36 degrees.

Now, let’s break down why this works. Imagine a triangle as a piece of a pizza slice. The angles are the corners of the slice. If you were to cut the slice straight down the middle, you’d end up with two right angles (90 degrees each). But since a triangle doesn’t have a straight cut, the angles adjust to make up for that missing piece. The total amount of angles will always be the same: 180 degrees!

We can classify triangles not only by their sides but also by their angles. To do this, we need to first understand the different types of angles that make up a triangle. This will help us determine if the triangle is acute, equiangular, obtuse, or right.

Let’s break down each type:

Acute Triangles: All three angles in an acute triangle are less than 90 degrees. Think of it as having three “sharp” corners.

Equiangular Triangles: These triangles have all three angles equal to each other. Since the sum of all angles in a triangle is always 180 degrees, each angle in an equiangular triangle is 60 degrees. You might also hear this type of triangle called an equilateral triangle.

Obtuse Triangles: An obtuse triangle has one angle that is greater than 90 degrees. This angle is considered “wide” or “rounded”.

Right Triangles: This type of triangle has one angle that measures exactly 90 degrees. This angle is often marked with a small square. The two shorter sides that form the right angle are called the legs and the longest side, opposite the right angle, is called the hypotenuse.

You can think of classifying triangles by their angles like sorting a collection of colorful candies. Each shape (acute, equiangular, obtuse, right) represents a different type of candy, and you’re carefully grouping them based on their unique characteristics.

You can create an exterior angle by extending one side of the triangle. The exterior angle is formed by the extended side and the adjacent side of the triangle.

Let’s look at it visually:

Imagine a triangle with three angles: angle A, angle B, and angle C.
Now, extend one side of the triangle, say side BC.
The extension creates a new angle, let’s call it angle D.
Angle D is the exterior angle formed at vertex C.

Here’s the key: The exterior angle is equal to the sum of the two non-adjacent interior angles of the triangle. In our example, angle D is equal to angle A + angle B.

This relationship is a fundamental property of triangles, and it’s a useful tool for solving problems involving angles. Understanding this concept allows you to find missing angles or prove relationships between angles within a triangle.

Remember: The exterior angle is always supplementary to the adjacent interior angle. This means that the exterior angle and its adjacent interior angle add up to 180 degrees. In our example, angle D and angle C add up to 180 degrees.

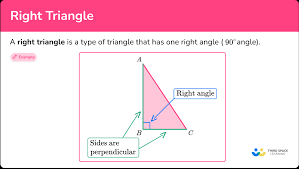
A right angle triangle is a special type of triangle with one angle measuring 90 degrees, which is also known as a right angle. This unique feature sets it apart from other triangles.

Let’s dive deeper into what makes a right angle triangle so interesting.

Imagine a straight line, like the edge of your table. Now, imagine another line that meets the first line at a perfectly square corner, forming a 90-degree angle. This is the basis for a right angle triangle. The two lines that form the 90-degree angle are called the legs of the triangle. The third side, which connects the ends of the legs, is called the hypotenuse. The hypotenuse is always the longest side of a right angle triangle.

You might be thinking, “How do I know if a triangle has a right angle?” Well, there’s a simple way to check. If you can draw a square perfectly inside the angle, then it’s a right angle. Think of it like fitting a square block into a corner. If it fits snugly, it’s a right angle!

Right angle triangles are super useful in math, especially in geometry and trigonometry. They’re the foundation for many important formulas and concepts. So, the next time you see a triangle with a square corner, remember – it’s a right angle triangle, and it holds a special place in the world of shapes!

Rules of a Triangle- Sides, angles, Exterior angles,

Learn the rules and properties of triangles, such as the sum of interior angles, the triangle inequality theorem, and the relationship between sides and angles. Use interactive tools and worksheets to practice and Mathwarehouse.com

Angles of a Triangle – Math Steps, Examples & Questions

Learn how to find the sum of interior and exterior angles of a triangle, and how to use angle facts to solve missing angle problems. See examples of scalene, right and isosceles Third Space Learning

Select the correct set of angles that can form a triangle. – BYJU’S

Solution. The correct option is C 45o, 45o, and 90o. We know that the sum of three angles of a triangle is 180°. Option (A): Three angles given are 44°, 44°, and 112°. Adding them, BYJU’S

Triangle Angle. Calculator | Formula

Learn how to find the angle of a triangle using different methods and formulas. The web page also explains the triangle angle sum theorem, exterior angle theorem, Omni Calculator

2.3: Triangles – Mathematics LibreTexts

Triangles can be classified by the characteristics of their angles and sides, and triangles can be compared based on these characteristics. The sum of the measures of the interior angles of any Mathematics LibreTexts

Classifying Triangles by Angles | ChiliMath

Math Solver. Worksheets. New. Triangle Classification by Angles. Classifying Triangles by Angles. Aside from classifying triangles by their sides, triangles can also be classified ChiliMath

Triangles | Geometry (all content) | Math | Khan Academy

About this unit. You probably like triangles. You think they are useful. They show up a lot. What you’ll see in this topic is that they are far more magical and mystical than you ever Khan Academy

Constructing Triangles – Math is Fun

Learn how to construct a triangle with two angles and one side, or one angle and two sides, or three sides. See examples and constructions for different types of triangles. Math is Fun