Are you looking for an answer to the topic “what is the only variable in the poisson probability formula“? We answer all your questions at the website barkmanoil.com in category: Newly updated financial and investment news for you. You will find the answer right below.
Keep Reading

What is the variable in the Poisson probability formula?
Poisson Formula.
Suppose we conduct a Poisson experiment, in which the average number of successes within a given region is μ. Then, the Poisson probability is: P(x; μ) = (e–μ) (μx) / x! where x is the actual number of successes that result from the experiment, and e is approximately equal to 2.71828.
What is a Poisson random variable?
A discrete random variable X is said to have a Poisson distribution, with parameter , if it has a probability mass function given by: where. k is the number of occurrences (
Introduction to Poisson Distribution – Probability Statistics
Images related to the topicIntroduction to Poisson Distribution – Probability Statistics

For which random variable is Poisson distribution applied?
Explanation: Poisson Distribution along with Binomial Distribution is applied for Discrete Random variable.
Are the variables in a Poisson trial counted?
The Poisson distribution often fits count data. It fits well when the mean of the variable is equal to its variance.
Which one of these variables is a binomial random variable?
Top Answer
First case – the women taller than 68 inches. Second case – the women is not taller than 68 inches. So, it can be said that the variable stating number of women taller than 68 inches in a sample of randomly selected 5 women is the binomial random variable. Thus, the correct option is c).
Which one of these variables is a continuous random variable?
A continuous random variable is one which takes an infinite number of possible values. Continuous random variables are usually measurements. Examples include height, weight, the amount of sugar in an orange, the time required to run a mile.
What is Poisson equation explain?
Poisson’s Equation (Equation 5.15. 5) states that the Laplacian of the electric potential field is equal to the volume charge density divided by the permittivity, with a change of sign.
See some more details on the topic what is the only variable in the poisson probability formula here:
Poisson Distribution | Introduction to Statistics
Read this as “X is a random variable with a Poisson distribution.” The parameter is μ (or λ); μ (or λ) = = the mean for the interval of interest. Example 2:.
stats 5 and 6 Flashcards | Quizlet
What is the only variable in the Poisson probability formula? x. A listing of all possible outcomes of an experiment and their corresponding probabilities …
Poisson distribution – Wikipedia
The CDF is discontinuous at the integers of k and flat everywhere else because a variable that is Poisson distributed takes on only integer values. Notation …
Poisson Distribution – an overview | ScienceDirect Topics
2. The exact probability that a Poisson random variable X with mean μ is equal to a is given by the formula.
What is the parameter of Poisson distribution?
The Poisson distribution is defined by the rate parameter, λ, which is the expected number of events in the interval (events/interval * interval length) and the highest probability number of events.
What variable can take only a countable number of values?
A random variable can be either discrete or continuous. Discrete random variables take on a countable number of distinct values.
What are binomial variables?
This is a specific type of discrete random variable. A binomial random variable counts how often a particular event occurs in a fixed number of tries or trials. For a variable to be a binomial random variable, ALL of the following conditions must be met: There are a fixed number of trials (a fixed sample size).
Which of the following statement is true for Poisson distribution?
In a Poisson distribution, mean and variance are equal – this statement is true.
What is the variance of a Poisson distribution with mean λ?
Var(X) = λ2 + λ – (λ)2 = λ. This shows that the parameter λ is not only the mean of the Poisson distribution but is also its variance.
An Introduction to the Poisson Distribution
Images related to the topicAn Introduction to the Poisson Distribution
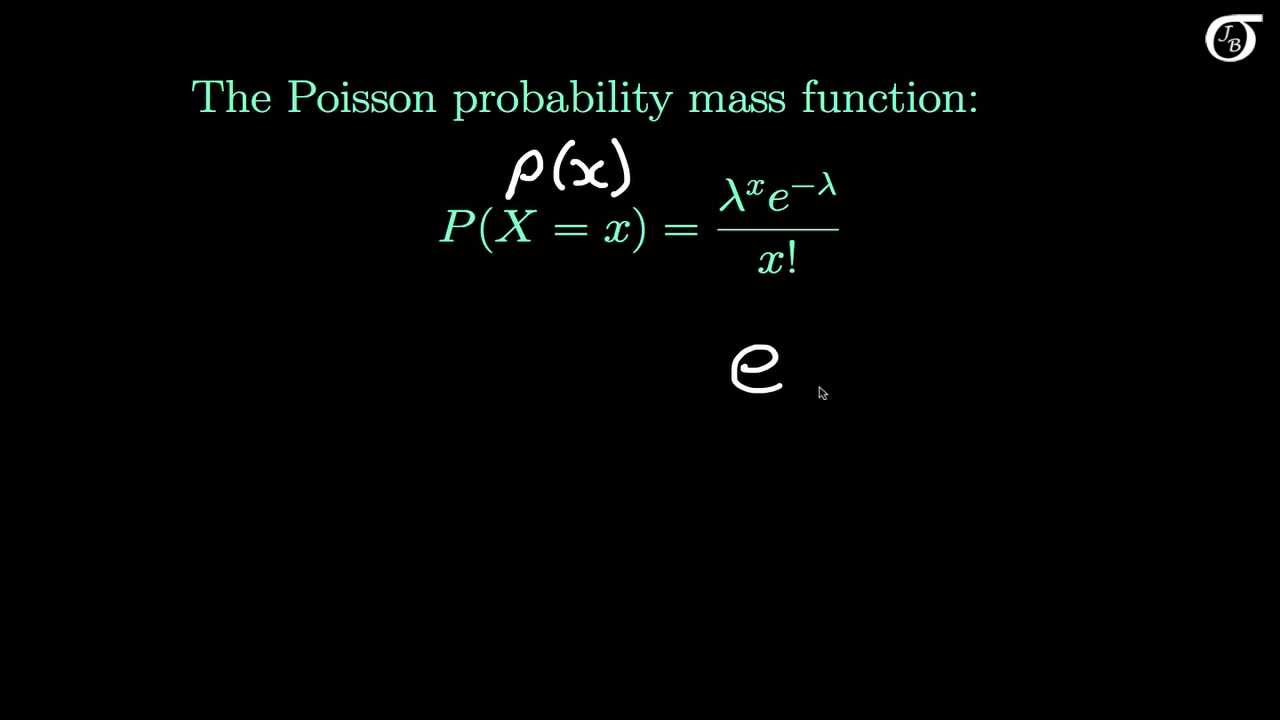
Is time a count variable?
Time is a continuous variable. You could turn age into a discrete variable and then you could count it. For example: A person’s age in years.
Is a count variable ordinal?
It’s also a count – for most analyses you might want to do it’s not rescalable. When a variable is ratio it is always ordinal and interval, so usually we simply say it is ratio. Indeed, treating a ratio (or count) variable as ordinal will often be a bad idea – classifying continuous or count variables usually is.
What is a ratio variable in statistics?
Ratio variable is the peak type of measurement variable in statistical analysis. It allows for the addition, interaction, multiplication, and division of variables.
Is a Poisson random variable discrete or continuous?
The Poisson distribution is a discrete function, meaning that the variable can only take specific values in a (potentially infinite) list.
How do you find the binomial random variable?
The mean of a binomial distribution with parameters N (the number of trials) and p (the probability of success for each trial) is m=Np . The variance of the binomial distribution is s2=Np(1−p) s 2 = Np ( 1 − p ) , where s2 is the variance of the binomial distribution.
What is the expected value of the random variable?
The expected value of a random variable is denoted by E[X]. The expected value can be thought of as the “average” value attained by the random variable; in fact, the expected value of a random variable is also called its mean, in which case we use the notation µX. (µ is the Greek letter mu.)
Which of the following is a discrete variable?
The answer is the gender of each student in a psychology class is an example of a discrete variable.
Which is a discrete random variable?
A discrete random variable can be defined as a type of variable whose value depends upon the numerical outcomes of a certain random phenomenon. It is also known as a stochastic variable. Discrete random variables are always whole numbers, which are easily countable.
Which of the following values is not the value of the probability of the random variable?
0.05can be the value of the probability of the random variable . Thus, 1.01 can not be the value of the probability of the random variable. Option A is correct.
How do you solve Poisson’s equation?
- Step 1: Separate VariablesEdit. Consider the solution to the Poisson equation as u ( x , y ) = X ( x ) Y ( y ) . …
- Step 2: Translate Boundary ConditionsEdit. As in the solution to the Laplace equation, translation of the boundary conditions yields: …
- Step 3: Solve Both SLPsEdit. …
- Step 4: Solve Non-homogeneous EquationEdit.
PB19: The Poisson Random Variable
Images related to the topicPB19: The Poisson Random Variable

Which equation is called as Poisson’s equation?
Dirichlet Problem
H(r,r0) has a physical interpretation, it is the potential arising from a so called image charge, thus this method of solving Poisson’s equation with F(r,r0) is also called the method of image charges.
Where does Poisson’s equation come from?
Poisson’s equation is derived from Coulomb’s law and Gauss’s theorem. It is a par- tial differential equation with broad utility in electrostatics, mechanical engineer- ing, and theoretical physics. It is named after the French mathematician, geometer and physicist Siméon-Denis Poisson (1781-1840).
Related searches to what is the only variable in the poisson probability formula
- for a binomial distribution the mean is 4 0 and n 8 what is for this distribution
- Poisson distribution examples
- Poisson distribution formula
- poisson distribution formula
- poisson distribution la gi
- let the random variable x be a poisson distribution with mean of 0 8 find the probability that x 1
- Poisson distribution Excel
- Poisson distribution calculator
- poisson distribution calculator
- Let the random variable X be a Poisson distribution with mean of 0.8 find the probability that X > 1
- Poisson distribution là gì
- poisson distribution excel
- poisson distribution examples
- poisson distribution table
Information related to the topic what is the only variable in the poisson probability formula
Here are the search results of the thread what is the only variable in the poisson probability formula from Bing. You can read more if you want.
You have just come across an article on the topic what is the only variable in the poisson probability formula. If you found this article useful, please share it. Thank you very much.