Are you looking for an answer to the topic “python lu factorization“? We answer all your questions at the website barkmanoil.com in category: Newly updated financial and investment news for you. You will find the answer right below.
Keep Reading

Is LU factorization the same as LU decomposition?
Answer and Explanation: LU factorization is another name as LU decomposition, as the both titles indicate that a given matrix can be expressed in two smaller matrices, which…
What is L and U in LU decomposition?
LU Decomposition Method or Factorisation
Step 1: Generate a matrix A = LU such that L is the lower triangular matrix with principal diagonal elements being equal to 1 and U is the upper triangular matrix.
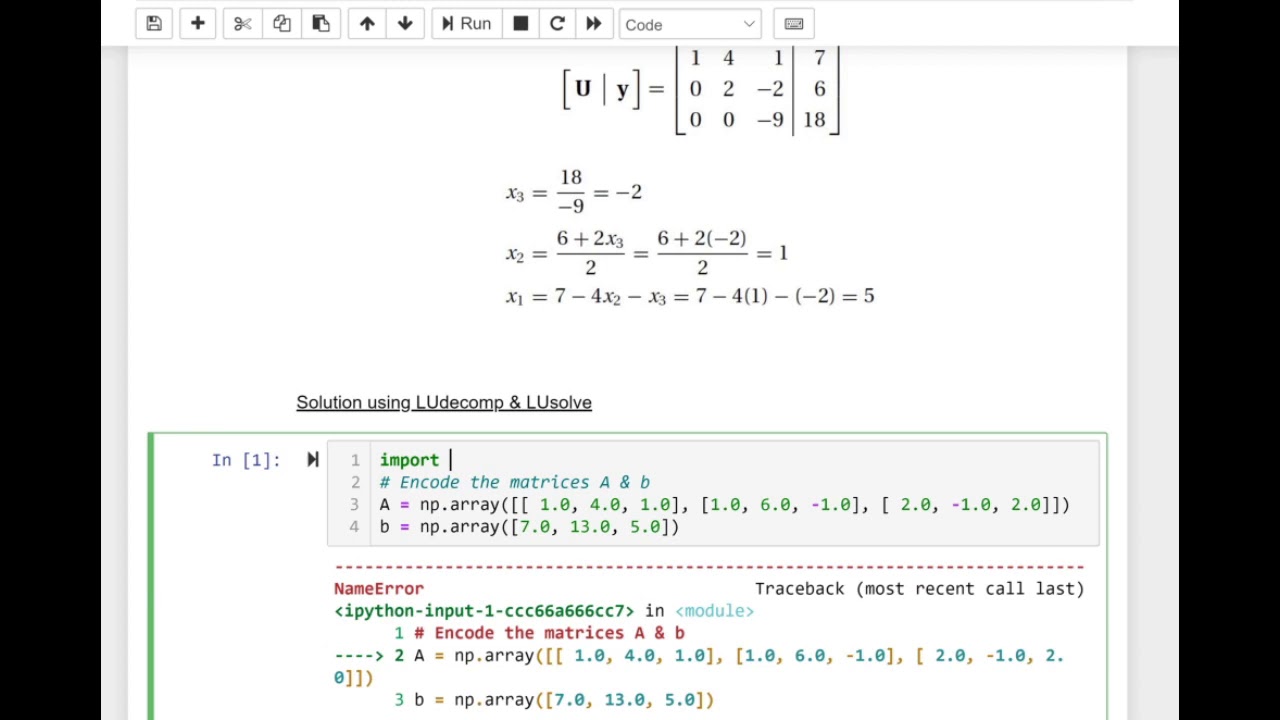
LU Decomposition in Python
Images related to the topicLU Decomposition in Python

What is LU factorization used for?
LU decomposition is a better way to implement Gauss elimination, especially for repeated solving a number of equations with the same left-hand side. That is, for solving the equation Ax = b with different values of b for the same A.
Which Python library contains implementation of LU decomposition?
Compute pivoted LU decomposition of a matrix.
What is permutation matrix in LU decomposition?
LU factorization is a way of decomposing a matrix A into an upper triangular matrix U , a lower triangular matrix L , and a permutation matrix P such that PA = LU . These matrices describe the steps needed to perform Gaussian elimination on the matrix until it is in reduced row echelon form.
What is Doolittle method?
Doolittle’s method provides an alternative way to factor A into an LU decomposition without going through the hassle of Gaussian Elimination. For a general n×n matrix A, we assume that an LU decomposition exists, and write the form of L and U explicitly.
Do all matrices have an LU factorization?
A square matrix is said to have an LU decomposition (or LU factorization) if it can be written as the product of a lower triangular (L) and an upper triangular (U) matrix. Not all square matrices have an LU decomposition, and it may be necessary to permute the rows of a matrix before obtaining its LU factorization.
See some more details on the topic python lu factorization here:
LU Decomposition in Python and NumPy | QuantStart
In this article we will present a NumPy/SciPy listing, as well as a pure Python listing, for the LU Decomposition method, which is used in certain …
LU Factorization – John T. Foster
The SciPy function scipy.linalg.lu performs a PLU decomposition. However, we can’t …
Doolittle Algorithm : LU Decomposition – GeeksforGeeks
In numerical analysis and linear algebra, LU decomposition (where ‘LU’ stands for ‘lower upper’, and also called LU factorization) factors a …
Matrix Decompositions — Computational Statistics in Python
LU stands for ‘Lower Upper’, and so an LU decomposition of a matrix · where · Now, LU decomposition is essentially gaussian elimination, but we work only with the …
What is the difference between Doolittle and crout method?
Doolittle’s method returns a unit lower triangular matrix and an upper triangular matrix, while the Crout method returns a lower triangular matrix and a unit upper triangular matrix. So, if a matrix decomposition of a matrix A is such that: A = LDU. A = (LD)U.
Why factorization method is preferred over other methods?
Explanation: Factorization method is preferred over other methods because it involves less number of calculations.
What is triangular factorization?
1.2 Triangular factorizations of an n × n matrix. The goal of this section is to prove that any n × n matrix A has the factorization PA = LU where P is an n × n permutation matrix, L is an n × n unit lower triangular matrix, and U is an n×n upper triangular matrix.
Can you Lu Factorize a non square matrix?
In my textbook, there is some information about LU factorization of square matrix A, but not about non-square matrix. How can LU factorization be used to factorize non-square matrix? Yes.
2.3 – Doolittle’s LU Decomposition (example code) – Engineering Numerical Method w/ Python 3
Images related to the topic2.3 – Doolittle’s LU Decomposition (example code) – Engineering Numerical Method w/ Python 3
Is Lu Factorisation unique?
LU factorization is not unique.
What is advantage and disadvantage of using LU decomposition method over basic Gauss elimination method?
| Method | Advantages | Disadvantages |
|---|---|---|
| LU decomposition | Efficient if one set of linear equations is repeatedly solved with different inhomogeneous terms (e.g., in the inverse power method.) | Less efficient and more cumbersome than Gauss elimination if used only once. |
What is pivoting in LU decomposition?
Pivoting for LU factorization is the process of systematically selecting pivots for Gaussian elimina- tion during the LU factorization of a matrix. The LU factorization is closely related to Gaussian elimination, which is unstable in its pure form.
How do you do LU decomposition with partial pivoting?
- Step one-select the maximum absolute value to be a new pivot.
- Step Two- Write the proper permutation matrix p12 that causes the swap.
- Step Three-Create an elimination matrix M1.
- Step Four-make a swap between row 2 and row 3.
- Step Five-Find the final upper matrix.
How do you find the determinant of a lower triangular matrix?
The determinant of a lower triangular matrix (or an upper triangular matrix) is the product of the diagonal entries. In particular, the determinant of a diagonal matrix is the product of the diagonal entries.
What is SciPy Linalg?
Advertisements. SciPy is built using the optimized ATLAS LAPACK and BLAS libraries. It has very fast linear algebra capabilities. All of these linear algebra routines expect an object that can be converted into a two-dimensional array.
How do you reverse a matrix in Numpy?
We use numpy. linalg. inv() function to calculate the inverse of a matrix. The inverse of a matrix is such that if it is multiplied by the original matrix, it results in identity matrix.
Is Lu Factorisation unique?
LU factorization is not unique.
What is crout’s method?
In linear algebra, the Crout matrix decomposition is an LU decomposition which decomposes a matrix into a lower triangular matrix (L), an upper triangular matrix (U) and, although not always needed, a permutation matrix (P). It was developed by Prescott Durand Crout.
Python Programming – Computing the LU Decomposition | Linear Algebra
Images related to the topicPython Programming – Computing the LU Decomposition | Linear Algebra

How do you do LU decomposition with partial pivoting?
- Step one-select the maximum absolute value to be a new pivot.
- Step Two- Write the proper permutation matrix p12 that causes the swap.
- Step Three-Create an elimination matrix M1.
- Step Four-make a swap between row 2 and row 3.
- Step Five-Find the final upper matrix.
What is triangular factorization?
1.2 Triangular factorizations of an n × n matrix. The goal of this section is to prove that any n × n matrix A has the factorization PA = LU where P is an n × n permutation matrix, L is an n × n unit lower triangular matrix, and U is an n×n upper triangular matrix.
Related searches to python lu factorization
- python convert to factor
- lu decomposition with pivoting python
- Gaussian elimination python numpy
- qr decomposition python
- QR decomposition Python
- python generate number list
- lu decomposition python
- python divide example
- LU factorization
- lu factorization without pivoting python
- back substitution algorithm python
- lu factorization python numpy
- python factorise a number
- gaussian elimination python numpy
- lu decomposition calculator
- python generator number of items
- python divide large numbers
- lu factorization with partial pivoting python
- incomplete lu factorization python
- LU decomposition Python
- lu factorization
- python generator return list
- python clean phone number
- scipy lu solve
Information related to the topic python lu factorization
Here are the search results of the thread python lu factorization from Bing. You can read more if you want.
You have just come across an article on the topic python lu factorization. If you found this article useful, please share it. Thank you very much.