Why Don T Parallel Lines Ever Meet | Why Can’T Two Parallel Lines Intersect Each Other?

Why Parallel Lines Don’t Intersect

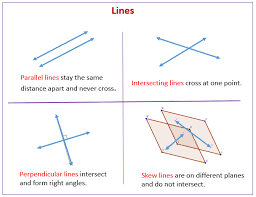
Parallel lines are lines that lie in the same plane and never intersect. This means they will always stay the same distance apart, no matter how far you extend them. Think of train tracks—they are parallel and will never cross.

You might wonder why this is true. It’s because of the way we define parallel lines. The definition itself says they don’t intersect! But let’s explore this a bit further.

Imagine you have two lines that are almost parallel. They might seem like they’re going to intersect if you only look at a small portion of them. But if you extend those lines, you’ll find that they eventually diverge and never cross.

Now, what about projective geometry? Projective geometry is a way of looking at geometry that allows for parallel lines to intersect at infinity. It’s a bit of a mind-bender, but it helps us understand that parallel lines can actually meet in a sense, just not in the typical Euclidean plane.

Think of it like this: Imagine you’re driving down a straight road. The road looks like it goes on forever. In a sense, the edges of the road, which are parallel, meet at a point called the “horizon” which is at infinity.

This concept of parallel lines meeting at infinity might sound strange, but it’s a very useful concept in geometry and other areas of math. It allows us to see the world in a new way and understand how shapes and lines relate to each other.

So, while it might seem like parallel lines can intersect, they actually can’t in the Euclidean plane. However, in the projective plane, they can meet at a point that’s infinitely far away.

Parallel lines never intersect. They maintain a constant distance from each other at every point. This means that they will never meet, no matter how far they are extended.

Imagine two straight lines drawn on a piece of paper. If these lines are parallel, they will always remain the same distance apart. You could extend these lines indefinitely in both directions, but they would never touch. This concept of parallel lines not intersecting is a fundamental principle in geometry. It’s a bit like two trains running on parallel tracks – they might travel for miles and miles, but they will never collide because they stay on their separate paths.

Think about it this way: if two lines were to intersect, it would mean they are no longer parallel. Parallel lines, by definition, must maintain a consistent distance between them, which prevents them from ever crossing paths.

In Euclidean geometry, the one we learn in school, parallel lines never meet. This means they don’t have any common points. This is the very definition of parallel lines: They always maintain the same distance apart and will never intersect.

Let’s break down why this is so important. Imagine a perfectly flat surface, like a sheet of paper. If you draw two lines that are always the same distance apart, no matter how far you extend them, those lines are parallel. This concept is fundamental to understanding shapes and space in Euclidean geometry.

Now, you might be wondering, what if we change the rules? In non-Euclidean geometry, things get a little more interesting. Imagine a sphere, like the Earth. On a sphere, the lines of longitude are all parallel at the equator, but they eventually meet at the North and South poles. This is because the surface of a sphere is curved, and the rules of Euclidean geometry don’t apply.

So, while in the familiar world of Euclidean geometry, parallel lines never meet, in other geometries, things can get a little more complex! But the basic idea of parallel lines as lines that maintain the same distance apart remains a key concept in geometry.

Parallel lines are lines that never intersect, and they form the same angle when they cross another line. This means that they are always the same distance apart, no matter how far they extend.

Think of it this way: imagine two train tracks. They run parallel to each other, meaning they never touch. You can imagine extending those tracks infinitely in both directions, and they still wouldn’t touch. That’s because they are parallel – they have the same angle and stay the same distance apart.

This concept of parallel lines is fundamental in geometry and has many applications in real life. For example, architects use parallel lines when designing buildings to ensure that walls are straight and windows are aligned. Engineers use parallel lines when building bridges and roads to ensure that structures are stable and safe.

The concept of parallel lines also plays a crucial role in understanding the geometry of shapes. For example, a rectangle is defined as a quadrilateral with four right angles and two pairs of parallel sides. This means that each pair of opposite sides is parallel and therefore never intersects.

So, when it comes to parallel lines, remember that they are always the same distance apart and never intersect. This fundamental concept helps us understand the world around us, from the design of buildings to the geometry of shapes.

Let’s explore why parallel lines never meet!

We know the distance between two parallel lines is always the same. Think of it like this: if you have two long, straight roads running side by side, the distance between them will always be the same, no matter how far down the road you go.

Since the distance is constant, it can never become zero. And if the distance between the lines is never zero, that means the lines themselves can never touch or intersect. That’s why we say parallel lines never meet.

To visualize this, imagine drawing two lines on a piece of paper. If you draw them so that they are always the same distance apart, they will never cross. No matter how far you extend the lines, they will always stay parallel.

This concept of constant distance is a key characteristic of parallel lines. It’s what makes them so interesting and useful in geometry.

Imagine you have a bunch of tiny arrows pointing in different directions, all representing the electric field. Electric lines of force are like imaginary lines that connect these arrows. These lines show the direction the electric field would push a positive charge. Now, think about what would happen if two of these lines crossed each other.

At the point where they intersect, we would have two arrows pointing in different directions. This is impossible because an electric field at any given point can only have one direction. The electric field at that point would be pulling the positive charge in two different directions at the same time, and that’s just not physically possible!

Think of it like this: Imagine trying to push a ball with two hands in opposite directions. The ball won’t go anywhere because the forces are canceling each other out. Similarly, if two electric lines of force intersect, they would be pulling the charge in opposite directions, causing a conflict.

That’s why electric lines of force never intersect – it’s simply not allowed by the laws of physics. They always flow smoothly and never cross paths.

That’s right! Parallel lines never intersect or meet at any point. This makes the statement true.

Let’s break this down a little more. Imagine you’re drawing two lines on a piece of paper. If these lines are parallel, they will always maintain the same distance from each other, no matter how far you extend them. This means they’ll never cross paths.

Think of it like train tracks. They run side by side, never crossing. That’s a perfect example of parallel lines in action!

Another way to understand this is by thinking about the angle between the two lines. Parallel lines have the same angle, which means they are essentially “going in the same direction.” Since they are always pointing in the same direction, they can’t possibly meet.

So, the next time you see two lines that are running alongside each other, remember: they are parallel and will never intersect!

When an object is placed at the focal point of a lens, the light rays emanating from it become parallel after passing through the lens. These parallel rays never actually meet in the real world, but the concept of them meeting “at infinity” is a useful way to describe their behavior.

Think of it this way: Imagine you are looking at a distant object, like a star. The light rays from that star reach your eye as parallel lines. You know that these rays actually originated from a very far distance, but your eye perceives them as meeting at a single point – the star. This point where the rays appear to converge is considered to be at “infinity.”

While the rays never truly intersect, the concept of them meeting at infinity is a helpful tool in understanding how lenses work. It allows us to simplify calculations and visualize the paths of light rays. For instance, when we say the rays “meet at infinity,” it means they will travel in parallel directions for a very long distance, effectively behaving as if they were converging at an infinitely distant point. This idea is crucial in understanding how lenses form images and how light behaves in different optical systems.

In standard geometry, parallel lines never intersect. This means they will never meet, no matter how far they are extended.

Imagine two lines on a piece of paper. If these lines are parallel, they will always maintain the same distance from each other. You could draw them across the entire page, and they would never touch.

Let’s consider a simple example: the line x = 1 and the line x = 2. These lines represent vertical lines on a graph. The line x = 1 passes through all points where the x-coordinate is 1, while the line x = 2 passes through all points where the x-coordinate is 2. Since a point can’t have two different x-coordinates at the same time, these lines will never intersect.

Now, let’s dive a bit deeper into the concept of parallel lines and why they never meet. The core idea is that parallel lines have the same slope. The slope of a line tells us how steep it is. Think of it as the “angle” at which the line is tilted. If two lines have the same slope, they are essentially tilted at the same angle. This means they are traveling in the same direction and will never cross paths.

For example, if you have two lines, one with a slope of 2 and another with a slope of 2, they will be parallel. Even if one line is higher than the other, they will never converge. They will always maintain the same distance apart.

It’s important to remember that we are talking about standard geometry here. There are some more complex geometries, like non-Euclidean geometries, where the rules are different. In those systems, parallel lines might behave differently, and they might even intersect. But in the everyday geometry we use to understand the world around us, parallel lines simply do not meet.

We often think of parallel lines as lines that never meet, and that’s true in what we call Euclidean geometry – the kind of geometry we learn in school. But there’s a whole world of other geometries out there, and in some of these geometries, parallel lines don’t always behave the way we expect!

Spherical geometry, which takes place on the surface of a sphere, is a great example. Imagine drawing lines on a globe. Two lines of longitude, for instance, will always meet at the North and South poles, even though they appear parallel at the equator. In spherical geometry, any two lines will eventually intersect.

Think about it this way: if you were to walk along the equator, you would eventually end up back where you started, having traveled in a circle. Since you’ve come back to your starting point, the lines you’re walking on must have met!

It’s like a closed system, where everything connects. Imagine a globe. Every point on the globe is connected to every other point by at least one line. This makes it impossible for any two lines on the globe to remain truly parallel.

The concept of parallel lines is a great reminder that geometry can be a lot more exciting and complex than we might initially think!

In Euclidean geometry, parallel lines never intersect. This is because parallel lines are defined as straight lines in a plane that extend indefinitely in both directions and never meet.

Even at infinity, parallel lines remain parallel. This might seem counterintuitive because the concept of infinity can be tricky to grasp. However, the definition of parallel lines in Euclidean geometry is clear: they never intersect, regardless of how far they are extended.

Imagine two parallel lines drawn on a piece of paper. You can extend these lines as far as you like, but they will always remain the same distance apart. Even if you could extend them to infinity, they would still be parallel and never intersect.

This is a fundamental principle of Euclidean geometry, which is the geometry that we learn in school. However, in other geometries, such as non-Euclidean geometry, it is possible for parallel lines to intersect.

For example, in spherical geometry, which is the geometry of the surface of a sphere, all lines are great circles, which are circles that divide the sphere into two equal hemispheres. On a sphere, all great circles intersect at two points, even if they are “parallel” in the sense that they share the same direction at a particular point.

However, for the purposes of everyday geometry and our understanding of the world around us, we use Euclidean geometry. In Euclidean geometry, parallel lines never intersect, even at infinity.

Let’s talk about parallel and non-parallel lines. In geometry, parallel lines never intersect, which means they always maintain the same distance from each other. Imagine two train tracks running side by side – they’re a perfect example of parallel lines.

Non-parallel lines, on the other hand, do intersect at some point. Think of two roads crossing each other. These are non-parallel lines because they meet at a specific point.

But what about the idea of parallel lines meeting at infinity? This is where projective geometry comes into play. It’s a way of thinking about geometry where we add a special “point at infinity” to our usual geometric space.

Here’s the cool part: In projective geometry, we can imagine parallel lines meeting at this point at infinity. It’s like saying that if we were to extend those parallel lines forever, they would eventually meet at this special “point at infinity.”

Now, this concept of a “point at infinity” might seem strange, but it’s actually a very powerful tool in mathematics. It allows us to think about geometry in a more unified way and solve problems that are difficult to handle with traditional Euclidean geometry.

For example, in projective geometry, we can think of any two lines as intersecting, either at a regular point or at this “point at infinity.” This simplifies some geometric problems and opens up new ways to understand shapes and spaces.

Do parallel lines merge at infinity? – Mathematics Stack Exchange

Euclid had defined parallel lines to be straight lines in a plane that “being produced indefinitely in both directions” never intersect; and accordingly, will never meet (or “merge”) even at infinity. Mathematics Stack Exchange

Can parallel lines meet? – Mathematics Stack Exchange

As Daniel Rust notes, the definition of parallel is that two lines don’t meet. What some people are trying to point out as examples are situations where lines cannot be parallel. Mathematics Stack Exchange

Question Corner — Do Parallel Lines Meet At Infinity?

If you are talking about ordinary lines and ordinary geometry, then parallel lines do not meet. For example, the line x =1 and the line x =2 do not meet at any Department of Mathematics at the University of Toronto

If diverging rays never meet, why do parallel rays

Lines are curves of degree 1, so two lines meet at exactly one point. The lines are called parallel if the line at infinity passes through that intersection point. But the “line at infinity” depends on your Physics Stack Exchange

1.4: Parallel Lines – Mathematics LibreTexts

Two lines are parallel if they do not meet, no matter how far they are extended. The symbol for parallel is \(||\). In Figure \(\PageIndex{1}\), Mathematics LibreTexts

Parallel (geometry) – Wikipedia

In geometry, parallel lines are coplanar infinite straight lines that do not intersect at any point. Parallel planes are planes in the same three-dimensional space that never meet. Wikipedia

Parallel Lines (Geometry) | Brilliant Math & Science Wiki

According to the axioms of Euclidean geometry, a line is not parallel to itself, since it intersects itself infinitely often. However, some authors allow a line to be parallel to itself, so that “is parallel to” forms an equivalence Brilliant

Parallel Lines – Definition, Math Steps, Examples

Parallel lines are lines that never intersect because they are always the same distance apart. For example, Parallel lines are seen in many common 2D shapes. For example, Each side of a square is made of a Third Space Learning

Parallel Lines – MathBitsNotebook(Geo)

Parallel lines are coplanar lines (in the same plane) that never intersect (never cross each other). The slope of a line measures its steepness (or its angle from the horizontal). Lines that are parallel have the same MathBitsNotebook