Do Sin And Arcsin Cancel Each Other Out?

Let’s break down the relationship between arcsin (also known as sin^-1) and sin.

It’s true that they can seem to “cancel” each other out under certain conditions, but it’s important to understand why and when this happens.

The key is domain. arcsin and sin are *inverse functions*. This means that they “undo” each other. Think of it like putting on your shoes and then taking them off—you end up back where you started. But there’s a catch!

To make sure the “undoing” works perfectly, arcsin needs to know the *correct starting point*. This is where the domain comes in.

arcsin is designed to only give you angles between -π/2 and π/2 (or -90° and 90° in degrees). If you feed arcsin an angle outside of this range, it won’t be able to “cancel” sin properly.

Here’s an example:

Let’s say you have sin(π/3) = √3/2. If you then take arcsin(√3/2), you get π/3 back. This works because π/3 is within the domain of arcsin.

But, if you have sin(4π/3) = -√3/2, and you take arcsin(-√3/2), you get -π/3, *not* 4π/3. This is because -π/3 is within the arcsin domain, and it’s the angle that gives you -√3/2 when you take its sine.

So, in a nutshell:

arcsin and sin “cancel” each other out when the angle you’re working with is within the arcsin domain (between -π/2 and π/2).
* Outside of this domain, arcsin will still give you an angle, but it might not be the same angle you started with.

Think of it like this: arcsin is like a map that only shows a specific region. If you’re looking for a place outside of that region, the map won’t be able to help you find it.

The arcsin function, also known as asin or sin⁻¹, is the inverse of the sine function. In simpler terms, if you know the sine of an angle, the arcsine tells you what the angle is.

Think of it like this: the sine function takes an angle as input and gives you the ratio of the opposite side to the hypotenuse in a right triangle. The arcsine function does the opposite—it takes that ratio as input and gives you the angle.

For example, if the sine of an angle is 0.5, then the arcsine of 0.5 is 30 degrees. This is because the sine of 30 degrees is 0.5.

Here’s a more detailed explanation:

Sine function (sin): Takes an angle (in radians or degrees) as input and outputs a value between -1 and 1. This value represents the ratio of the opposite side to the hypotenuse in a right triangle.
Arcsine function (arcsin): Takes a value between -1 and 1 as input and outputs an angle (in radians or degrees). This angle corresponds to the angle whose sine is equal to the input value.

The arcsine function is important in various fields, including trigonometry, calculus, and physics. It helps us solve problems involving angles and trigonometric functions.

Let’s talk about inverse functions and how they relate to canceling each other out.

Think of inverse functions as opposites. If a function f takes an input x and does something to it, its inverse function f⁻¹ undoes that something. They work in perfect harmony to bring you back to the original input.

Here’s the cool part: f(x) and f⁻¹(x) are like a perfect pair. They cancel each other out! This means that if you apply f to x and then apply f⁻¹ to the result, you’ll get back your original x. It’s like taking a step forward and then taking a step back – you end up in the same place.

We can write this mathematically as:
f(f⁻¹(x)) = x
f⁻¹(f(x)) = x

For example, consider the function f(x) = x + 2. The inverse function of f(x) is f⁻¹(x) = x – 2. Let’s say you start with the input x = 5.

f(5) = 5 + 2 = 7. This means that f takes the input 5 and adds 2 to it, resulting in 7.
f⁻¹(7) = 7 – 2 = 5. Now, f⁻¹ takes the output 7 and subtracts 2, bringing you back to your original input 5.

f(f⁻¹(5)) = f(5 – 2) = f(3) = 3 + 2 = 5.

f⁻¹(f(5)) = f⁻¹(5 + 2) = f⁻¹(7) = 7 – 2 = 5.

As you can see, in both cases, the function and its inverse cancel each other out, returning you to your original input.

This “cancellation” property is a fundamental characteristic of inverse functions. It tells us that inverse functions are truly inverses, undoing the operation performed by the original function.

You’re right! Cosine and inverse cosine functions, also known as arccosine, have a special relationship. They are inverses of each other, which means they “undo” each other’s actions.

Let’s break down what this means:

– Cosine takes an angle as input and gives you the ratio of the adjacent side to the hypotenuse in a right triangle.
– Inverse cosine takes a ratio (between -1 and 1) as input and gives you the angle that corresponds to that ratio.

So, if you take the cosine of an angle and then apply the inverse cosine to the result, you’ll get the original angle back.

Think of it like putting on a pair of shoes and then taking them off. You end up back where you started!

This cancellation only works when you apply the inverse cosine function to the output of the cosine function. If you apply the cosine function to the output of the inverse cosine function, you won’t get the original input back.

Here’s a simple example to illustrate:

1. Cosine: Let’s say the angle is 60 degrees. The cosine of 60 degrees is 0.5.
2. Inverse cosine: Now, let’s take the inverse cosine of 0.5. This gives us 60 degrees, which is our original angle!

This principle is used to solve equations involving cosine functions. If you have an equation with the cosine of an unknown angle, you can isolate the angle by applying the inverse cosine function to both sides of the equation.

The inverse sine function, arcsin, takes the ratio, Opposite Side / Hypotenuse Side, and produces the angle θ. It’s also written as sin^-1.

Let’s clarify what arcsin means. It’s like the opposite of the sine function. Think of it this way: The sine function takes an angle and tells you the ratio of the opposite side to the hypotenuse in a right triangle. Arcsin does the opposite! It takes that ratio and gives you the angle.

So, if you know the ratio of the opposite side to the hypotenuse and want to find the angle, you use arcsin. For example, if the ratio is 0.5, arcsin(0.5) would give you 30 degrees.

It’s important to note that arcsin is NOT the same as sin^-1.

The notation sin^-1 can be confusing because it looks like the reciprocal of sin. However, it’s not. Sin^-1 actually refers to the inverse function.

Arcsin and sin^-1 are simply two different ways of writing the same thing – the inverse sine function.

Remember, arcsin or sin^-1 takes a ratio and produces an angle, while sin takes an angle and produces a ratio. They are inverses of each other.

To summarize, arcsin is a vital tool for finding angles in trigonometry when you know the ratio of the opposite side to the hypotenuse. Understanding the concept of the inverse sine function is crucial for solving various problems in trigonometry and other areas of mathematics and science.

arcsin and cosecant are not the same thing in trigonometry. They are different functions with unique definitions and applications.

Let’s break down the differences. arcsin, also known as sin^-1, is the inverse of the sine function. It answers the question, “What angle has a sine of _x_?” In other words, if you know the sine of an angle, arcsin will tell you the angle itself.

Cosecant, abbreviated as csc, is a reciprocal trigonometric function. It’s defined as the reciprocal of the sine function: csc(x) = 1/sin(x). So, cosecant gives you the ratio of the hypotenuse to the opposite side in a right triangle, while sine gives you the ratio of the opposite side to the hypotenuse.

Here’s a simple analogy: think of them as opposites in a way. arcsin takes a sine value and finds the angle, while cosecant takes an angle and finds the reciprocal of its sine value.

To illustrate further, let’s say you have a right triangle where the sine of an angle is 0.5. Using arcsin, you would find that the angle itself is 30 degrees. Now, using cosecant, you would find the value of csc(30°), which is 2. This means the ratio of the hypotenuse to the opposite side is 2:1.

In essence, arcsin and cosecant are distinct functions with different purposes and applications in trigonometry. While they are both related to the sine function, they operate on different inputs and provide different outputs.

Let’s clear up some common confusion about inverse sine! You might see it written as arcsin, asin, or even sin^-1. It’s important to remember that asin is NOT the same as sin 1.

Here’s the deal: inverse sine is a function that finds the angle whose sine is a given value. For example, arcsin(0.5) would give you the angle whose sine is 0.5, which is 30 degrees (or π/6 radians).

It’s easy to get confused because the notation sin^-1 looks like an exponent, but it’s actually just a way of representing the inverse function. So, sin^-1(x) is not the same as (sin(x))^-1, which would be 1/sin(x) or csc(x) (cosecant).

arcsin has a domain of [-1, 1] and a range of [-π/2, π/2]. This means that you can only input values between -1 and 1 into the arcsin function, and the output will always be an angle between -π/2 and π/2.

Now, why is sin(arcsin(x)) not always x? Think of the sine function as a wave. It repeats itself over and over again, so there are multiple angles that can have the same sine value. Since arcsin only gives you the angle in the range of [-π/2, π/2], sin(arcsin(x)) will only equal x if x is within that range.

For example, if x = 0.5, then arcsin(0.5) = π/6, and sin(π/6) = 0.5. But if x = -0.5, then arcsin(-0.5) = -π/6, and sin(-π/6) = -0.5. However, there are other angles whose sine is -0.5, like -5π/6 or 7π/6. In these cases, sin(arcsin(-0.5)) would not equal -0.5 because arcsin(-0.5) only gives you the angle in the range of [-π/2, π/2].

In summary, asin, arcsin, and sin^-1 all refer to the inverse sine function, which is a function that finds the angle whose sine is a given value. It’s important to understand the domain and range of arcsin and how it relates to the sine function itself. Don’t confuse arcsin with 1/sin(x) or (sin(x))^-1.

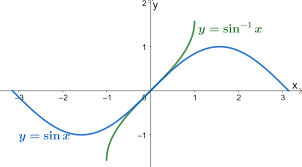
The arcsine function, also known as the inverse sine function, is the inverse of the sine function. This means it reverses the input and output of the sine function.

The arcsine function has a domain of -1 to 1 and a range of -π/2 to π/2. The graph of the arcsine function is shown below.


You can see that the arcsine function is odd. This means that arcsine(-x) = -arcsine(x). You can see this from the symmetry of the graph about the origin (0, 0).

Deeper Dive into the Arcsine Function

Let’s break down what this means in a more practical way. Imagine you have a right triangle. You know the length of the opposite side and the hypotenuse. You want to find the angle. This is where the arcsine function comes in handy.

The arcsine function takes the ratio of the opposite side to the hypotenuse (which is the sine of the angle) and gives you the angle itself. For example, if the ratio of the opposite side to the hypotenuse is 0.5, the arcsine function will tell you that the angle is 30 degrees.

The arcsine function is a powerful tool for solving problems involving right triangles, trigonometry, and even more complex mathematical concepts.

Here’s how it works:

Input: The input of the arcsine function is a value between -1 and 1. This value represents the sine of an angle.
Output: The output of the arcsine function is an angle between -π/2 and π/2. This angle is the angle whose sine is the input value.

Let me give you a real-world example. Imagine you’re trying to find the height of a tree. You measure the distance from the tree to where you’re standing (the adjacent side) and you measure the angle from the ground to the top of the tree (the angle). Using the sine function, you can calculate the height of the tree.

But what if you know the height of the tree and the distance to the tree, and you want to find the angle? That’s where the arcsine function comes in. You can use the arcsine function to find the angle that corresponds to the ratio of the opposite side (the height of the tree) to the hypotenuse (the distance from the tree to where you’re standing).

Let’s talk about the inverse sine function, also known as arcsine and written as sin⁻¹x or arcsin(x). Think of it like this: the sine function takes an angle and gives you a ratio, while the inverse sine function does the opposite. It takes a ratio and gives you the angle.

Here’s a visual breakdown:

Sine Function: You input an angle (like 30 degrees) and get a ratio (like 0.5).
Inverse Sine Function: You input a ratio (like 0.5) and get an angle (like 30 degrees).

The graph of the inverse sine function, y = sin⁻¹x, is interesting. It’s a bit different from the standard sine curve. Here’s what you need to know:

Domain: The domain of the inverse sine function is the same as the range of the sine function, which is -1 ≤ x ≤ 1. This means the input to the inverse sine function must be a ratio between -1 and 1.
Range: The range of the inverse sine function is our restricted domain for the sine function, which is -π/2 ≤ y ≤ π/2. This means the output of the inverse sine function is an angle between -π/2 and π/2 (or -90 degrees to 90 degrees).

Why the restricted range? The sine function isn’t one-to-one over its entire domain, meaning there are multiple angles that can produce the same ratio. To ensure the inverse sine function has a single output for every input, we restrict its range to the interval -π/2 ≤ y ≤ π/2.

Think of it like this: if you were to graph the sine function, you’d see it repeats its values over and over again. By restricting the inverse sine function’s range, we’re essentially picking one specific angle (within the restricted range) for each ratio.

Let me illustrate with an example:

sin(30°) = 0.5
sin(150°) = 0.5

Both 30° and 150° have the same sine value (0.5). To make the inverse sine function work properly, we pick the angle in the restricted range, which is 30°.

So, when you take the inverse sine of 0.5, you get:

sin⁻¹(0.5) = 30°

This is how the inverse sine function works and why its range is restricted. It’s all about ensuring a unique angle for each ratio, making the inverse sine function a reliable tool in trigonometry and other fields.

You can’t calculate arcsin (0.98) using basic trigonometry. It’s a bit tricky!

Here’s why:

arcsin (x), also known as sin^-1(x), gives you the angle whose sine is *x*.
* The domain of arcsin (x) is [-1, 1], meaning the input *x* has to be between -1 and 1.
* You can’t just find an angle like 45º or 3π/4 that has a sine of 0.98.

So, how do you find arcsin (0.98)?

The easiest way is to use a calculator! It has a special button for arcsin. Just type in 0.98, press the arcsin button, and you’ll get the answer in degrees or radians, depending on your calculator’s setting.

Let’s talk a bit more about why this is a bit more complex:

In precalculus, you work mostly with the unit circle and familiar angles like 30º, 45º, 60º, and their radian equivalents. These angles have nice, easily calculated sine values (like √2/2). However, 0.98 is not a “nice” value like that. It’s a decimal that doesn’t correspond to a simple angle on the unit circle.

To find the exact angle for arcsin (0.98), you’d need to use advanced techniques from calculus. These involve things like Taylor series expansions, which are powerful tools for approximating functions. But that’s definitely beyond the scope of basic trigonometry!

So, in short, if you need to find arcsin (0.98), a calculator is your best friend! It does all the complicated math for you so you can focus on understanding the concept.

Let’s talk about the arcsine function, also known as sin⁻¹ or asin. It’s the inverse function of the sine function, but it has some interesting quirks.

You’re right to be curious about the domain of arcsine. It’s not defined for all real numbers. Arcsine only works for values between -1 and 1. This is because the sine function, which arcsine reverses, only outputs values within this range.

Think of it this way: sine takes an angle and gives you a ratio. Arcsine does the opposite. It takes a ratio (between -1 and 1) and tells you the angle that creates it. Since the sine function can only produce ratios within this range, arcsine can only accept those same ratios as input.

The reason for this restriction is to ensure that the arcsine function has a well-defined, single-valued output. The sine function is periodic, meaning it repeats its values over and over again. If arcsine weren’t restricted to a specific range, it would have multiple outputs for a single input, which wouldn’t be useful.

To avoid this ambiguity, we limit the output of the arcsine function to the range [-π/2, π/2] (or [-90°, 90°], in degrees). This is called the principal value of the arcsine function.

Now, you mentioned arcsin(sin(d ⋅ x)) = d ⋅ x for -π/2 ≤ d ⋅ x ≤ π/2. This is absolutely correct! As long as d ⋅ x falls within this restricted domain of arcsine, the equation holds. The arcsine function essentially “undoes” the sine function, leaving you with the original input, d ⋅ x.

In summary, the domain of arcsine is [-1, 1]. It’s the set of all possible ratios that can be generated by the sine function. We also need to consider the principal value of arcsine, which is limited to [-π/2, π/2] to ensure a single, well-defined output.

Remember, arcsine is a powerful tool, but it’s important to understand its limitations and how its domain influences its behavior.

Will this equation with $\\sin$ and $\\arcsin$ cancel?

Arcsine has a domain of values $y$ where $-1 \leq y \leq 1$, which means if we take $y = \sin(x)$ our values of $x$ are restricted by $-\pi/2 \leq x \leq \pi/2$. So as long as your constant $d$ is such that $zd = x$ where $x \in [-\pi/2, \pi/2]$ then we do know Mathematics Stack Exchange

Intro to inverse trig functions (article) | Khan Academy

We can also express the inverse sine as arcsin ‍ , the inverse cosine as arccos ‍ , and the inverse tangent as arctan ‍ . This notation is common in computer programming Khan Academy

19.1: The functions of arcsin, arccos, and arctan

These values together with the fact that the inverse sine is odd, that is \(\sin^{-1}(-x)=-\sin^{-1}(x)\), provides us with examples of its function values. Mathematics LibreTexts

Simple Trig Equations – Why is it Wrong to Cancel Trig Terms?

In the following problem, I first did it using a cancellation of sin2θ s i n 2 θ, working shown below, which gave the wrong answer. Having looked at the question Mathematics Stack Exchange

Inverse trigonometric functions review (article) | Khan Academy

I think you are confusing sine and arcsine. The domain of arcsin(x) is [-1, 1], and neither 45º nor 3π/4 is in that set. However, sin(45º) and sin(3π/4) are both √2/2. At this level, Khan Academy

8.1: Inverse Trigonometric Functions – Mathematics LibreTexts

Katherine Yoshiwara. Los Angeles Pierce College. We have been using the calculator keys \ (S I N^ {-1}, C O S^ {-1}\), and \ (T A N^ {-1}\) to find approximate values Mathematics LibreTexts

Inverse Trig Functions – Millersville University of

Sine and arcsine are inverses, so they undo one another — but you have to be careful! can’t be , because always returns an angle in the range . Example. sites.millersville.edu

2.4.3: Composition of Trig Functions and Their Inverses

Then, we need to find \(\sin \dfrac{\pi}{4}\), which is \(\dfrac{\sqrt{2}}{2}\). So, the above properties allow for a short cut. K12 LibreTexts

10.6: The Inverse Trigonometric Functions

The next pair of functions we wish to discuss are the inverses of tangent and cotangent, which are named arctangent and arccotangent, respectively. First, we restrict f (x) = \tan (x) to its Mathematics LibreTexts